В огромном саду Геометрии каждый найдёт букет себе по вкусу.
Давид Гильберт
«Точка – это то, что не имеет частей», – говорил Евклид. Современный математик посчитал бы эти слова пусть примитивным, но довольно точным определением «объекта нулевого измерения». Точка, оставленная карандашом на бумаге или острие булавки – вот эти «объекты» в реальной жизни. Сфера нулевого измерения – это и есть точка.
Нить, проволока и любая иная линия – это уже одномерные предметы: у них есть длина. Сфера в пространстве одного измерения – это две точки на прямой: центр этой одномерной сферы лежит посередине между ними.
Представители двумерного мира имеют и длину, и ширину – это ленты, куски ткани, листы бумаги. Окружность, граница двумерного круга – вот что такое сфера в пространстве двух измерений.
И, наконец, кубы, пирамиды, дома, корабли и самолеты так же, как и мы с вами, входят в неисчислимую армию «трёхмерцев», обладающих вдобавок к длине ширине еще и высотой. У них есть объем. Сфера в трехмерном пространстве – это шар, «обычная» сфера.
Но вот что любопытно. Проволоку можно сломать, лист бумаги разрезать, а куб распилить. И при этом получается, что одномерный объект, линия, разделяется объектом нулевого измерения – точкой. Двумерная плоскость делится надвое одномерной линией, а трехмерный куб – двумерной плоскостью. Иными словами, границей «разлома» тела служит какое-то другое тело, измерение которого на единицу ниже.
Что же тогда служит границей четырехмерной сферы?
Зайдем с другого конца. Если точку «протащить» по бумаге, то получится линия. Линия, в свою очередь, «заметает» плоскость – получается квадрат. Вытянем квадрат из плоскости – сделаем куб. Это уже третье измерение. Но что же такое надо сделать с кубом, чтобы обратить его в четырехмерное тело? И как его себе представить?

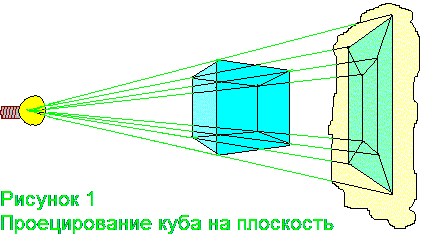
А что мы делаем, чтобы изобразить на плоском листе бумаге трехмерный куб? Мы проецируем его на плоскость. Получается два квадрата один в другом, соединенные вершинами (рис. 1).
Так же спроецируем и четырёхмерный куб (если это можно назвать кубом)! Мы получим по аналогии два куба, один в другом, и снова вершины попарно соединены. Вот он, посланец четвертого измерения, вернее, не сам он, а его проекция на плоскость (Рис. 2).
И точно также, рассуждая по аналогии, мы можем отдаленно представить себе четырехмерную сферу. Если спроецировать глобус на плоскость, то проекции двух его половин наложатся одна на другую, и Нью-Йорк окажется где-то в центре нашей Сибири. Проецируя глобус, мы пропускаем одну его полусферу сквозь другую и соединяем их проекции, круги, только по границе – окружности (как квадраты по вершинам). Проекция гиперсферы – два шара, прошедшие один через другой и соединенные только по внешним поверхностям. Конечно, вообразить все это нелегко, но мистического тут нет.
Еще один гость из иных миров носит имя «четырёхмерный симплекс». Симплекс – это простейшая из всех возможных фигур. Добавляя каждый раз всего по одной точке, мы пробегаем по ступеням лестницы размерностей. Одна точка – это нульмерный симплекс. Он живет, как уже говорилось, в нулевом измерении. Две точки определяют отрезок -- одномерный симплекс. Измерение – первое. Третья точка превращает линию в треугольник – двумерный симплекс. Ещё точка – и вот перед нами тетраэдр. Это уже простейшее из всех трехмерных тел – трехмерный симплекс. Но вот добавлена пятая точка. Эта необычная конструкция состоит из пяти тетраэдров. Все вместе они отделяют четырёхмерный симплекс от всего остального четырёхмерного пространства точно так же, как, как шесть граней куба отделяют его от остального трёхмерного пространства, а три стороны треугольника ограничивают его на плоскости.
Но что дает нам уверенность, что гиперкуб или «старший» из симплексов не принадлежит к нашему трехмерному миру? Существует один простой тест, основанный на формуле, выведенный ещё Леонардом Эйлером (а так же Декартом и Лейбницем). Эта формула истинно топологическая, потому что имеет дело не с размерами, углами или площадями, а лишь с числом вершин, ребер и граней любой геометрической фигуры.
Г + В = Р + 2
То есть число граней (Г) плюс число вершин (В) равно числу ребер (Р) плюс 2. Проверьте правильность этой формулы на какой угодно фигуре – кубе, пирамиде, тетраэдре, икосаэдре, произвольном многограннике, теле самой замысловатой формы. При любых деформациях любой из них формула Эйлера верна.
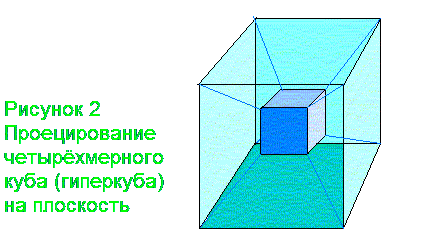
Но возьмите гиперкуб (Рис. 2): 24 стороны, 16 вершин, 32 ребра и сверх того 8 трехмерных граней – вот то геометрическое богатство, которым он обладает. Простейшие арифметические действия убедят вас, что гиперкуб пришёл к нам в гости из сложнейшего четырёхмерного мира, для него несправедлива формула Эйлера.
Итак, знакомство состоялось. Так и хочется задать «четырёхмерцам» традиционный вопрос: «Ну, как там?» Но гиперкуб молчит всеми своими восьмьюдесятью элементами, симплекс тоже безмолвствует, и нам остается лишь еще раз прибегнуть к испытанному приему – разбежаться перед прыжком: раз надо исследовать свойства четвертого измерения – отступим пока во второе.
В 1884 году Эдвин Эбботт издал книгу, которая называлась «Флатланд – «Плосколяндия» («Двумерия»), и хотя она была чисто математической по содержанию, но вызвала много шума в разных кругах общества – автора упрекали даже в женоненавистничестве. И в самом деле, в воображаемой Плосколяндии, стране двух измерений, женщины были простейшей из фигур – прямой линией. Все остальные обитатели представляли собой различные многоугольники: рабочие и солдаты – треугольники, ремесленники – квадраты, джентльмены – пятиугольники, а священники были настолько многоугольными многоугольниками, что больше всего походили на круги. И вот в этот плоский, плоский, плоский мир является существо из третьего измерения – сфера. Квадрат (от его лица ведётся рассказ) увидел перед собой священника, который вёл себя самым противоестественным образом: он то раздувался, то сжимался. Сколько ни пыталась Сфера объяснить Квадрату, что все эти видимые им круги разного диаметра – это всё она одна, когда проходит сквозь Плосколяндию вверх и вниз, он так и не смог вообразить себе трехмерную сферу, пронизывающую его двухмерный мир.
Как можно убедить разумное существо, что ты посланец иных миров? Только продемонстрировав ему чудо. Здесь у нас с вами, как и у любого «трёхмерца», самые широкие возможности. Но что нам стоит вынуть плоскатика из его дома (а это просто замкнутая кривая), не разрушая его стен? Извлечь содержимое плоского яйца, не протыкая его скорлупы? Произвести трансплантацию сердца любому гражданину Плосколяндии, не вскрывая его грудной клетки? Да просто, наконец, приподнять любой предмет в этой стране над плоскостью и тем самым «выключить» его из жизни и даже из поля зрения? И пусть плоскатики сочиняют свои басни о своих «летающих тарелочках».
Если две Плосколяндии удалены друг от друга на тысячи световых лет, но плоская лента их мира извивается в пространстве так, что одни её участки оказываются поблизости один от другого, то мы легко можем перенести плоскатика из одной галактики в другую со скоростью, в тысячи раз превышающей «его» скорость света: ведь мы пронесем его через третье измерение. Такие сказочные возможности несёт в себе увеличение размерности мира всего на единицу. Это значит, что «четырёхмерцы» так же всемогущи по отношению к нам, как мы – по отношению к «двухмерцам». Скажем нам не под силу надеть левую на правую руку или правый ботинок – на левую ногу. Но «четырёхмерец» без труда мог бы унести на мгновение и перчатку, и ботинок в свое «лишнее» измерение и вернуть их оттуда симметрично отображенными. Первым до этого додумался в 1827 году Франц Фердинанд Мёбиус.
Вообще происхождение идеи четвёртого измерения связано с Платоном, самым крупным древнегреческим философом – идеалистом, имя которого было присвоено целой группе геометрических тел – вполне материальных, не несущих в себе даже тени идеалистического мировоззрения. Так вот именно Платон в своей «Республике» повествует о прикованных у входа в пещеру пленниках, которые могут видеть лишь её противоположную стену и на ней свои тени и тени предметов, случайно оказывающихся у них за спиной. Эта невыносимая жизнь длится столь долго, что несчастные, в конце концов, начинают считать тенями самих себя, да и весь мир кажется им миром теней некоего иного внеземного и более совершенного мира – мира идей.
Неоплатоники развили представление о реальном мире как о тени, отбрасываемой потусторонним миром. Есть мнение, что само выражение «четвёртое измерение» (quarta dimensio) появилось впервые в сочинении английского мистика, кембриджского неоплатоника Мора в его книге «Энхиридион Метафизикум», изданной в 1671 году.
Но попробуем остаться на почве реальных фактов. Наша мысль рвется в четвертое измерение, а освоили ли мы своё собственное, третье? В полной ли мере познали мы его геометрические свойства и все ли три пространственные координаты – длина, ширина и высота – нам одинаково близки и понятны?
Вот простейший пример. Дана замкнутая кривая – круг или квадрат. Требуется чисто умозрительно, без карандаша и бумаги, решить: можно ли соединить две точки – одну внутри кривой, другую вне её, но так, чтобы не пересечь замкнутой кривой.
Представив себе этот элементарный чертёжик, и немного поразмыслив, мы уверенно утверждаем, что задача невыполнима. Дело в том, что наш «внутренний взор» несёт в себе евклидову плоскость – лист бумаги. Конечно же, на листе не соединишь две точки, не перечеркнув кривую, охватывающую одну из них. Но кто говорил нам о типе поверхности, на которой предстоит решать задачу? А если это не плоскость, а, скажем, бублик или автомобильная шина – всё получается легко и просто.
Человек слишком привык к двумерному миру. Наша геометрическая интуиция тут никогда нас не подводит. Но как только дело доходит до пространственных представлений, она начинает хромать. Высоту дома оценить куда труднее, чем его длину и ширину. А сказать, как далеко находится самолет или облако, неподготовленный человек не может даже приблизительно. Третьей координатой – не то, что четвертой! – нам ещё овладевать и овладевать.
Причина тут не психологическая, а чисто физиологическая. Всё дело в устройстве наших глаз. Когда мы смотрим на удалённый предмет, особые мускулы изгибают хрусталик глаза – естественную линзу, чтобы изменить её фокусное расстояние и дать нам увидеть предмет отчетливо. Наводка на резкость фотокамеры – полная аналогия этому процессу, который в физиологии называется аккомодацией.
И ещё в каждом глазе есть группа из шести мускулов, которые поворачивают его таким образом, чтобы направления взгляда правого и левого глаза пересекались в одной точке. Это называется конвергенцией. Так создается бинокулярный эффект – мы видим мир объемным.
Восприятие третьего измерения сводится к ощущению усилия, которое мы испытываем при аккомодации каждого глаза, и к ощущению усилия, которое возникает в обоих глазах при их конвергенции. Оба эти ощущения мускульные, они совершенно непохожи на зрительные ощущения, которые позволяют нам воспринимать первое и второе измерения. Мы видим плоскую картину, улавливаем игру света и тени, краски, взаимное расположение фигур и цветовых пятен на ней – и всё это зрительные ощущения. Панорама же требует от наших глаз включить мускульный аппарат аккомодации и конвергенции, и мы мгновенно ощущаем его работу.
Человечество пошло не по пути овладения третьим измерением, а по пути его «приручения»: люди старались втиснуть объем в плоскость, изобразить окружающий мир на скале, песке или папирусе.
Вся беда в том, что мы сами живём в третьем измерении и поэтому смотрим на него «изнутри», наш объёмный мир мы видим как бы плоским. Звучит парадоксально, но поместите лист бумаги с нарисованной на нём Плосколяндией и всеми её обитателями точно на уровне глаз – и вы на секунду испытаете трагедию плоскатиков, обречённых жить в двух измерениях, но ощущать лишь одно. Ведь чтобы увидеть фигуру – квадрат ли, круг, им надо хоть немного «выскочить» из своей плоскости. Но это невозможно, и именно поэтому весь мир они воспринимают как одну сплошную «женщину» - прямую линию. Остаётся лишь обойти фигуру со всех сторон и ощупать её, но только представители «низших классов» в Плосколяндии могут позволить себе, да то изредка, столь вульгарное поведение. «Лучше плохо видеть, чем хорошо щупать!» - одна из первых заповедей воспитанного человека в этой стране. Плосколяндцы обладают третьим измерением, но только оно вне их восприятия – ведь их мир одной толщины.
Так не обладаем ли мы четвёртым измерением, несмотря на то, что даже третье не освоено еще нами полностью?
У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. Август Фердинанд Мёбиус, немецкий математик и астроном в своей работе «Об объеме многогранников» описал геометрическую поверхность, обладающую совершенно невероятным свойством: она имеет только одну сторону! Сделать её своими руками очень легко: надо лишь взять полоску бумаги и склеить её концы, предварительно повернув один из них на 180 градусов. И в руках окажется лист, или лента, Мёбиуса. Чтобы наглядно убедиться, что него действительно всего одна сторона, можно попробовать закрасить перекрученную ленту в два цвета – одним с внешней, а другим – с внутренней стороны. Ничего из этого не получится. Но зато муравью, ползущему по листу Мёбиуса, не надо переползать через его край, чтобы попасть на противоположную сторону.
Итак, односторонность. В геометрическом, разумеется, понимании этого слова, потому что в общечеловеческом смысле трудно представить себе более разностороннюю геометрическую фигуру. Американский физик Ричард Дэвис изобрёл электрическое сопротивление, обладающее нулевой реактивностью. Оно позволяет увидеть одностороннюю ленту Мёбиуса с несколько иной стороны.
Но сначала нужно склеить ещё один лист Мёбиуса и разрезать его ножницами вдоль на три части, отступив от любого из краев на треть ширины ленты. Получается ещё один лист Мёбиуса – поменьше, да и шириной всего в треть от первоначального, а в него продета длинная и тонкая лента, дважды перекрученная вдоль своей оси. Нужно покрасить «маленького Мёбиуса» и уложить с обеих сторон от него ленту так, чтобы получился лист Мёбиуса тройной толщины. Получится удивительная фигура. Две её крайние незакрашенные части, хотя они и сделаны из одной длинной ленты, тем не менее, нигде не смыкаются друг с другом, а просто лежат вдоль сторон третьей, закрашенной. Но каких сторон? Ведь центральная часть – это одностороння поверхность! Да и крайние, раз они повторяют её форму, тоже не что иное, как два листа Мёбиуса, которые обрели самостоятельность, обвившись вокруг своего цветного собрата.
Вот это и есть сопротивление с нулевой реактивностью. Но только изготавливают его – для простоты технологии – немного по-другому: к резиновой ленте с двух сторон приклеивают две тонкие алюминиевые полоски, а к ним припаивают выводы, через которые можно подать электрический ток. Затем всю конструкцию перекручивают на один оборот и соединяют в мёбиусов лист – он, естественно, будет трёхслойным. И вот теперь ток, проходя по полоскам, встретит на своем пути лишь так называемое «активное» сопротивление, то есть сопротивление самого материала – алюминия. «Реактивность» проводника с током, имеющего форму листа Мёбиуса, равна нулю.
«То, что я понял, прекрасно, из этого я заключаю, что остальное, чего я не понял, тоже прекрасно», -- высказался в своё время Сократ по поводу неясностей у Гераклита. Быть может, эти слова послужат утешением для того, кто не сумеет одолеть суть радиотехнического дебюта листа Мёбиуса. Хотя понять её не так уж невозможно. Есть простой, но в данном случае неприятный для радиотехников факт: каждое тело имеет форму и как-то располагается в пространстве. А потому оно ведет себя либо как маленький конденсатор – обладает собственной электрической ёмкостью и, значит, оказывает переменному току емкостное сопротивление, либо поступает подобно крохотному дросселю – тогда его сопротивление индуктивное. Оба эти сопротивления, оказываемые телом электрическому току, называют реактивными. И избавится от них, как и оттого, что у него есть какая-то форма, ни одно тело как будто не может.
Но «трижды толстый мёбиус» можно сделать по- разному – и из трёх отдельных частей, и всего из двух: короткой центральной и особым образом уложенной длинной заготовки, которая одна образует обе боковые стороны. Значит, ток в безреактивном сопротивлении дважды проходит по одному и тому же месту в пространстве, но оба раза в противоположных направлениях, пробегая по длинной ленте – алюминиевым полоскам, уложенным «восьмёркой» с двух сторон короткой резиновой полосы, служащей изолятором. Таким образом, реактивность реактивностью же и уничтожается. И потому такое закрученное сопротивление остается чисто активным, даже если изгибать его как угодно или помещать в любое внешнее поле.
В разное время и в разных странах зарегистрировано немало изобретений, в основе которых лежит всё та же односторонняя поверхность. Односторонность – одно из топологических свойств листа Мёбиуса.
Сама топология началась именно с листа Мёбиуса. Слово это придумал Иоганн Бенедикт Листинг, профессор Геттингенского университета, который в качестве первого примера предложил уже знакомую, единожды перекрученную ленту. Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать – делать с ней что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло – все её свойства остались неизменными. Для него не имеют никакого значения ни расстояния, ни углы, ни площади. А что же его интересует? Самые общие свойства фигур, которые не изменяются ни при каких преобразованиях, если только не случается катастрофы – «взрыва» фигуры. Поэтому иногда топологию называют «геометрией непрерывности». Она известна и под именем «резиновая геометрия», потому что топологу ничего не стоит поместить все свои фигуры на поверхность детского надувного шарика и без конца менять его форму, следя лишь за тем, чтобы шарик не лопнул. А то, что при этом прямые линии, например, стороны треугольника, превратятся в кривые, для тополога глубоко безразлично. Во всех окружающих его предметах он ищет некие важные только ему одному качества. Например, непрерывность. С топологической точки зрения круг неотличим от квадрата или треугольника, потому что их легко преобразовать один в другой, не нарушая непрерывности. На листе Мёбиуса любая точка может быть соединена с любой другой точкой. Разрывов нет – непрерывность полная.
Другое свойство – связность. Если квадрат полоснуть бритвой от стороны к стороне, то он, естественно, распадается на два отдельных куска. Точно так же любой удар ножом разделит яблоко на две части. Но вот чтобы разделить кольцо пополам, нужно уже два разреза. И два раза придется резать бублик. А телефонный диск можно десять раз рассечь ножом от одной замкнутой кривой до другой, а он всё равно останется единым целым. Поэтому любой тополог скажет, что квадрат и ромашка -- односвязны, кольцо и оправа от очков – двусвязны, а всяческие решетки, диски с отверстиями и подобные сложные фигуры – многосвязны. А лист Мёбиуса? Конечно, двусвязен, ведь будучи разрезан вдоль, он превращается не в два отдельных, а в одну целую ленту. Впрочем, если перекрутить ленту на два оборота, то лист становится односвязным. Такой лист, разрезанный вдоль, превращается в две ленты, продетые одна в другую. Три оборота – лента, разрезанная вдоль, завязывает сама себя в узел. Связность снова равна двум.
Связность принято оценивать числом Бетти, названным так в честь известного итальянского математика и физика. Иногда пользуются другой величиной -- эйлеровой характеристикой – с той же целью: определить число сквозных, от края и до края, разрезов, которое выдерживает фигура, не распадаясь при этом на части.
Лист бумаги – модель двусторонней односвязной (число Бетти равно единице) поверхности с одним краем. Его можно смять, но всё равно число краёв (и сторон) останется прежним. Но у сферы краёв нет. Нет их и у тора, говоря попросту, бублика. Зато нарисованное на бумаге кольцо имеет целых два края. А у мёбиусова листа один край, как и одна у него сторона. Сделайте его, из какой угодно эластичной резины и растяните до любых размеров – топологические свойства, этот незыблемый фундамент самого естества геометрической фигуры, останутся неизменными.
Следующее свойство – ориентированность. Это то, чего нет у листа Мёбиуса. Вообразите, что в нем заключен целый плоский мир, где есть только два измерения, а его обитатели – несимметричные рожицы, не имеющие, как и сам лист, никакой толщины. Если эти создания пропутешествуют по всем изгибам листам листа Мёбиуса и вернутся в родные пенаты, то обнаружат, что превратились в своё собственное зеркальное отображение. Конечно, если они живут в листе, а не на нём. Это удивительное явление можно наблюдать и на действующей модели плоского мира Мёбиуса – для этого надо сделать ленту из любого прозрачного материала.
И наконец, свойство, которое носит название «хроматический номер». Он равен максимальному числу областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими. Если каждую такую область выкрасить по-разному, то любой цвет должен соседствовать с любым другим. Так вот, на листе бумаги, даже если его склеить в кольцо, ещё никому не удалось расположить пять цветных пятен любой формы, которые имели бы всеобщую границу. И на сфере, и на цилиндре их может быть не более четырёх. Это значит, что хроматический номер этих поверхностей – четыре. А на бублике число соседствующих цветов равняется семи. Каков же хроматический номер листа Мёбиуса? Он, как это ни поразительно, равен шести. Видите ли, на ленте, склеенной, как положено, размещается всего четыре цвета, а стоит соединить её концы шиворот-навыворот – и непонятно, как находится место ещё для двух цветов!
Есть древняя неразрешимая задача. Надо соединить три дома с тремя колодцами, но так, чтобы жители каждого из домов могли ходить по воду в любой колодец и при этом пути их нигде не пересекались. Задача неразрешима на плоскости, а на торе, то есть бублике, например, всё получается просто.